Máš nějakou otázku?
Odeslat zprávu
Message sent zavřít
Statisticky neklasicky > Blog > Popisná statistika > Rozptyl a další míry variability

Rozptyl a další míry variability

1 komentář
charakteristiky_variability

Variabilitu lze vidět všude kolem nás. Jezdíte pravidelně do školy, či práce a vaše doba strávená na cestě se každý den lehce liší. Kupujete si k snídani pečivo a jeho váha určitě není pokaždé stejná. Určitá míra variability je v takových situacích naprosto normální. To, co může způsobit jisté problémy, jsou větší odchylky. Pokud na cestě do školy strávíte výrazně delší čas než obvykle, přijdete pozdě, stejně tak to bude s neobvykle malým kusem rohlíku, nebudete si ho chtít koupit. Pojďme se na variability podívat trochu víc do hloubky a vysvětlit si základní míry, kterými jsou například rozptyl, či směrodatná odchylka. 🙂

Míry variability nám říkají, jak jsou hodnoty v souboru rozptýleny okolo střední hodnoty. Nízká míra variability nám říká, že hodnoty mají tendenci být seskupeny blízko středu. Vysoká míra variability znamená opak (hodnoty jsou rozptýleny dále od středu) a je zde vyšší riziko výskytu odlehlých hodnot.

Variabilitu, podobně jako míry polohy, je možné měřit několika způsoby. Nejpoužívanějšími charakteristikami variability jsou rozptyl, směrodatná odchylka, rozpětí, mezikvartilové rozpětí a variační koeficient.

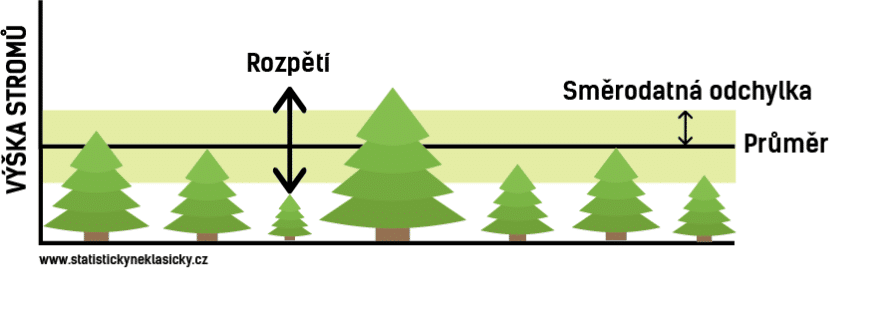
Rozpětí

Pojďme se podívat na tu nejednoduší míru a tou je rozpětí, přesněji variační rozpětí. Rozpětí se spočítá jako rozdíl maxima a minima. Stačí najít největší a nejmenší hodnotu a odečíst je od sebe.

R=x_{max}-x_{min}

 

Jedná se o rychlou a jednoduchou míru variability, která má jednu velkou nevýhodu a tou je vysoká citlivost na odlehlá pozorování.

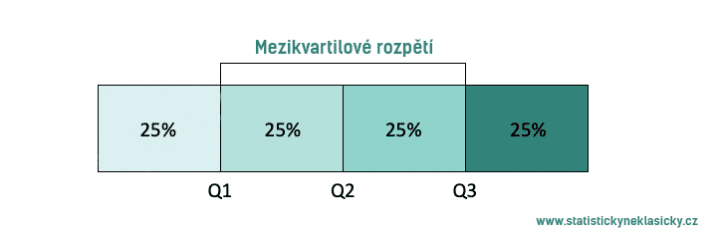
Mezikvartilové rozpětí

Zatímco variační rozpětí nám říká rozpětí celého souboru, mezikvartilové rozpětí nám řekne rozpětí pouze poloviny hodnot. Výpočet je poměrně jednoduchý, stačí najít horní a dolní kvartil a provést jednoduchou matematickou operaci. Dolní kvartil (Q1) je hodnota, pod kterou leží 25 % hodnot, zatímco horní kvartil (Q3) je hodnota, pod kterou leží 75 % hodnot. Výpočet se pak provede jako rozdíl horního a dolního kvartilu.

IQR=Q3-Q1

 

Mezikvartilové rozpětí je robustní mírou variability, podobně jako je medián robustní mírou polohy. Díky této vlastnosti je vhodnou mírou variability pro soubory s odlehlými hodnotami, či pro zešikmená rozdělení. Jak vyplývá z principu výpočtu, je počítán pouze z 50 % prostředních hodnot.

mezikvartilove rozpeti

Rozptyl

Zřejmě nejznámější míra variability a zároveň nejhůře interpretovatelná. Rozptyl se vypočítá jako průměr čtverců odchylek od průměru. Rozptyl vychází v kvadrátu (mocnině) a proto je těžké si pod jeho hodnotou něco představit.  Právě z tohoto důvodu je vhodnější k interpretaci použít směrodatnou odchylku, která se spočítá jako odmocnina z rozptylu.

Pro výpočet rozptylu je možné použít dva vzorce a to v závislosti na tom, zda máte data z populačního nebo výběrového souboru.

Rozptyl pro populaci:

\sigma ^{2}=\frac{\sum(x_{i}-\overline{x})^{2} }{n}

 

V případě populačního rozptylu se rozptyl zpravidla značí pomocí \sigma ^{2}, není to však pravidlem, je možné se setkat s různými typy označení. Z tohoto důvodu doporučuji koukat primárně na vzorec, než na symbol.

Rozptyl pro výběrový soubor:

U výběrových souborů používáme ve vzorci na rozptyl n – 1. Použití n by nám poskytlo zkreslený odhad, rozptyl by byl podhodnocený.

s^{2}=\frac{\sum(x_{i}-\overline{x})^{2} }{n-1}

 

Při výpočtu rozptylu jsou použity všechny hodnoty v souboru a je jednou ze základních charakteristik variability. Jeho nevýhodou je citlivost na odlehlá pozorování. Zároveň je velmi často využíván ve statistických testech a k posouzení homoskedasticity.

Ve výpočtu rozptylu umocňujeme rozdíly hodnot od průměru, tím zabráníme tomu, aby se hodnoty nad a pod průměrem vzájemně vyrušily. V důsledku toho je rozptyl vždy větší nebo roven nule. Pokud se chcete o jeho využití a výpočtu dozvědět více, doporučuji některý z online kurzů.

Směrodatná odchylka

Na řadu přichází královna celého článku a tou je směrodatná odchylka. Směrodatná odchylka je, jak už bylo zmíněno, odmocninou z rozptylu.

\sigma=\sqrt{\sigma ^{2}},s=\sqrt{s ^{2}}

 

Velikou výhodou je, že vychází v původních jednotkách proměnné a tedy ji můžeme snadno interpretovat. Například si představte, že čas vašeho příchodu má směrodatnou odchylku 6 minut. Znamená to, že typicky na schůzku přijdete +- 6 minut od domluveného času. Směrodatná odchylka nám v průměru řekne, jak daleko každá hodnota leží od průměru. Lze si ji snadno představit dle následujícího obrázku:

smerodatna_odchylka

Směrodatná odchylka je velmi užitečným nástrojem u proměnných, které mají normální rozdělení! Společně s průměrem nám dokážou říct, kde leží většina hodnot. Lze to také nazvat empirickým pravidlem. Platí, že:

  • Přibližně 68 % hodnot leží v rozmezí +/- 1 směrodatné odchylky od průměru.
  • Přibližně 95 % hodnot leží v rozmezí +/- 2 směrodatných odchylek od průměru.
  • Přibližně 99,7 % hodnot leží v rozmezí +/- 3 směrodatných odchylek od průměru.

Rozdělení je možné vidět v následujícím grafu normálního rozdělení:

Variační koeficient

Pojďme se podívat na poslední uvedenou míru variability, kterou je variační koeficient. Jedná se o relativní míru variability, která udává velikost směrodatné odchylky ve vztahu k jejímu průměru. Tato míra se používá k porovnání variability mezi různými skupinami.

Představte si, že chcete srovnat variability vah krav a lidí. Směrodatná odchylka hmotnosti krav by mohla být třeba kolem 200 kg a směrodatná odchylka hmotnosti lidí řekněme 25 kg. Nejde přeci na základě těchto údajů říct, že krávy mají vyšší variabilitu hmotnosti. Je nutné toto srovnání provést relativně a to právě pomocí variačního koeficientu. Tento příklad je trochu extrémní, ale věřím, že si díky němu zapamatujete důležitost variačního koeficientu 🙂

Variační koeficient se spočítá jako směrodatná odchylka dělená průměrem.

v_{x}=\frac{s}{\overline{x}}

 

Lze ho vyjádřit i procentuálně a to tak, že ho vynásobíme 100. Opět platí, že vyšší hodnota indikuje vyšší míru variability. Zde pozor, že variační koeficient může vyjít větší než 1 (100 %). V některých případech může být hodnota směrodatné odchylky větší než průměr. Je důležité zmínit, že variační koeficient není vhodný v případech, kdy se hodnota průměru blíží nebo rovná nule. Když je průměr blízký nule, tak má variační koeficient tendenci blížit se nekonečnu.

Na závěr se podívejme na nejčastější dotazy:

Kdy je rozptyl roven 0?

Pokud jsou všechny hodnoty v souboru stejné.

Jak spočítat rozptyl v Excelu?

Výběrový rozptyl se spočítá přes funkci VAR.S
Populační rozptyl přes funkci VAR.P

Pozor, že funkce neberou v potaz váhy (četnosti) hodnot.

Jak spočítat směrodatnou odchylku v Excelu?

Výběrovou směrodatnou odchylku lze spočítá přes funkci SMODCH.VÝBĚR.S
Populační směrodatnou odchylku přes funkci SMODCH.P

Pozor, že funkce neberou v potaz váhy (četnosti) hodnot.

Co použijete pro srovnání variability mezi více soubory?

Variační koeficient

Která míra variability je robustní?

Mezikvartilové rozpětí.

Co nám říká empirické pravidlo?

Empirické pravidlo (pravidlo 68-95-99,7) nám říká, kde leží většina hodnot v normálním rozdělení.

Jaký je rozdíl mezi směrodatnou odchylkou a rozptylem?

Směrodatná odchylka vychází v původních jednotkách a je odmocninou z rozptylu.

Pojď se o statistice dozvědět více a nauč se to, co opravdu potřebuješ!

Vyber si jeden z našich online kurzů!

CHCI ONLINE KURZ

Autorka:Adriana

Ahoj! Jmenuji se Adriana a pravděpodobně miluji statistiku. Pokud se zdržíš, určitě to propukne i u Tebe! Snažím se, aby studentům statistika dávala smysl a aby je učení bavilo. Na této stránce nečekej výuku, kterou Ti nabízí většina učebnic a škol. Snažím se to dělat jinak! Chci Ti pomocí online kurzů ukázat, že statistika není taková nuda, jak se říká (nebo zpívá), a pokud se ji naučíš, získáš nejenom dobrou známku, ale i mnohem lepší povědomí o světě a věcech kolem nás.

1 komentář