Testování hypotéz

V tomto článku si řekneme, co jsou to statistické hypotézy, jak s hypotézami pracovat a naučíme se některé základní pojmy. Testování statistických hypotéz nám umožňuje vyvozovat závěry o populaci na základě reprezentativního vzorku. Zpravidla není možné získat data z celé populace a právě proto používáme inferenční statistiku, která nám dovolí na základě vzorku dat vyvozovat závěry pro celý populační soubor.

Pojďme si celý postup ukázat na jednoduchém příkladu:

Pravidelně chodíte do své oblíbené pekárny a kupujete si k snídani skvělé jahodové koblihy. Po určité době máte pocit, že se velikost a tím i váha koblih změnila, ačkoli pekárna stále uvádí původní váhu 65 g. Jelikož se právě učíte statistiku, zkusíte si udělat svůj vlastní výzkum.

V pekárně si zakoupíte 40 koblih a zvážíte je. Průměrná váha vám vyjde 62,6 gramů a směrodatná odchylka 6,99 gramů. Hladinu významnosti zvolíte standardně 5 %. V rámci našeho testování budeme předpokládat normální rozdělení dat.

Zde je potřeba si uvědomit, že když se jedná o náhodný výběr 40 koblih, lze jen těžko předpokládat, že by vám průměrná váha vyšla přesně 65 gramů. Otázka však je, kdy je rozdíl mezi zjištěnou (62,6 gramů) a předpokládanou hodnotou (65 gramů) opravdu významný. K tomu nám již pomůže statistika.

Další údaje nejsou potřeba a můžeme se společně pustit do testování!

Vždy je nutné stanovit nulovou a alternativní hypotézu.

Nulová a alternativní hypotéza

Nulová hypotéza obvykle uvádí, že nedošlo k žádné změně, či že mezi proměnnými není závislost. Tedy například:

• Výsledky skupin jsou shodné.
• Mezi pohlavím a užitím návykových látek není významná závislost.
• Korelační koeficient je statisticky nevýznamný.
• Podíl voličů odpovídá předpokladu.

V našem příkladu nulová hypotéza tvrdí, že střední hodnota váhy koblih je 65 gramů. V případě jednovýběrových testů, což je i náš příklad, dáváme do nulové hypotézy vždy předpokládanou hodnotu (původní tvrzení). Nulovou hypotézu potom značíme jako H₀.

Alternativní hypotéza obvykle uvádí, že k nějaké změně došlo, například:

• Výsledky skupin jsou rozdílné.
• Mezi pohlavím a užitím návykových látek je významná závislost.
• Korelační koeficient je statisticky významný.
• Podíl voličů neodpovídá předpokladu.

U alternativních hypotéz máme menší rozšíření a to takové, že můžeme mít buď jednostrannou nebo oboustrannou alternativní hypotézu. V našem příkladu bychom se mohli ptát, zda se váha koblih významně snížila. V takovém případě by šlo o jednostrannou alternativní hypotézu (H₁: mí < 65 g), stejně tak pokud bychom se ptali, zda se váha zvýšila (H₁: mí > 65 g). Pokud se budeme ptát, zda došlo ke změně váhy, aniž bychom chtěli testovat, zda se má snížit, či zvýšit, tak se jedná o oboustrannou alternativní hypotézu (H₁: mí ≠ 65 g).  Jak jste si již mohli všimnout, tak alternativní hypotéza se zpravidla značí jako H₁ nebo H_A.

Chceme testovat, zda se váha změnila a tedy budeme pracovat s oboustrannou alternativní hypotézou.

H_{0}:\mu = 65
H_{1}:\mu \neq 65

Pojďme k dalšímu krok a tím je volba správného testu.

jednovýběrový test pro střední hodnotu

Typy testů a jejich volbu si vysvětlíme v nějakém dalším článku. V případě naší úlohy použijeme tzv. jednovýběrový test pro střední hodnotu a spočítáme testové kritérium (testovou statistiku). Výpočet lze vidět zde:

Výsledek testové statistiky nám zaokrouhleně vyšel -2.17.

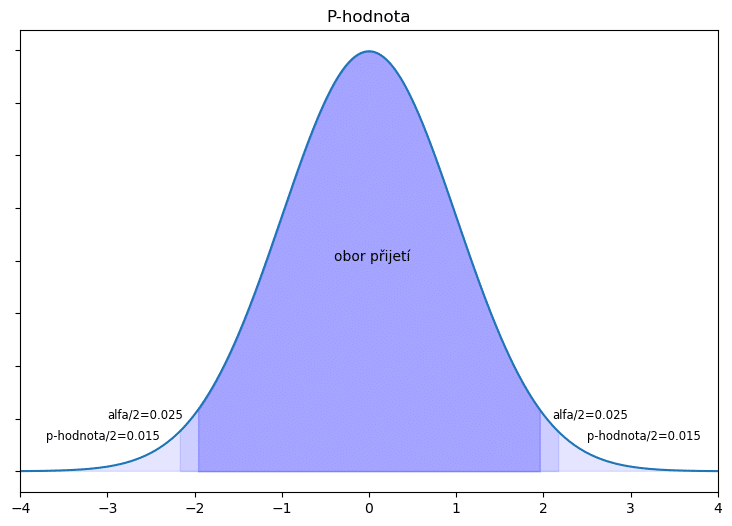
Nyní máme dvě možnosti, buď najdeme tzv. kritickou hodnotu nebo určíme p-hodnotu.

Pojďme si ukázat obě varianty. Jelikož naše data mají normální rozdělení (viz. náš příklad), můžeme si vše ukázat právě na křivce normálního rozdělení. (Pokud již o testování něco víte, tak bych jen ráda zmínila, že vzhledem k velikosti výběrového souboru je použito normální rozdělení, nad n > 30 je možné i při neznámém populačním rozptylu tuto aproximaci použít, kdyby byl vzorek menší, bylo by použito Studentovo t rozdělení. Výpočty a vysvětlení najdete v mnoha online kurzech).

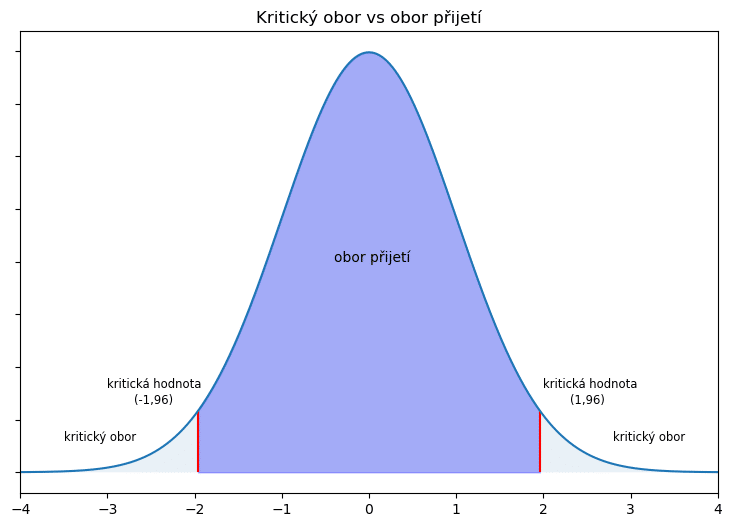
Kritická hodnota

Kritická hodnota je hranice mezi oborem přijetí a kritickým oborem. Testové statistiky, které překročí kritickou hodnotu, spadnou do kritického oboru. Pokud testová statistika spadne do kritického oboru, tak nulovou hypotézu zamítáme. Pokud testová statistika tuto hodnotu nepřekročí, je v oboru přijetí, tak nulovou hypotézu nezamítáte. Kritická hodnota vychází z použitého rozdělení (v našem případě normálního) a z hladiny významnosti, v případě některých rozdělení hrají roli i stupně volnosti.

Hladina významnosti

Hladinu významnosti lze definovat jako pravděpodobnost zamítnutí nulové hypotézy, ačkoli je H₀ pravdivá. Značí se zpravidla jako alfa (α) a představuje také chybu I. druhu. Například hladina významnosti 0,05 znamená, že je 5% pravděpodobnost, že dojde k nesprávnému zamítnutí nulové hypotézy (zamítnu H₀, ačkoli platí).  Čím nižší tato hladina je, tím je obtížnější H₀ zamítnout.

Jak určíme naši kritickou hodnotu?

Hladina významnosti je 5 %, tedy alfa=0,05. Používáme oboustrannou hypotézu, proto musíme naší hladinu významnosti vydělit dvěma, tím dostaneme hodnotu 0,025. Znamená to, že kritický obor bude tvořit na levé straně grafu 2,5 % a na pravé straně 2,5 %. Ve statistických tabulkách si pak najdeme kvantil normovaného normálního rozdělení (normální rozdělení s nulovou střední hodnotou) a budeme hledat hodnotu 0,975 (1-0,025), hledáme 0,975, jelikož hodnoty jsou zpravidla uváděny od hodnoty 0,5 (rozdělení je symetrické). Pro tuto pravděpodobnost nacházíme hodnotu 1,96, jedná se o kvantil normovaného normálního rozdělení a naší kritickou hodnotu. Pro hodnotu 0,025 by tak šlo o kritickou hodnotu -1,96. (Pozn. pro studenty ČZU, v tabulkách ČZU jsou uváděny automaticky hodnoty pro oboustranné hypotézy, tedy hodnotu 1,96 najdete pod pravděpodobností 0,95).

V grafu níže lze vidět obor přijetí, kritickou hodnotu a kritický obor. Pokud si vezmeme naší hodnotu -2,17 (případně ji klidně můžeme použít v absolutní hodnotě jako 2,17), tak lze krásně vidět, že spadá do kritického oboru a tedy nulovou hypotézu zamítáme a přijímáme hypotézu alternativní na 5% hladině významnosti.

Další způsob jak lze provést testování statistických hypotéz je pomocí p-hodnoty.

P-hodnota

Ohledně interpretace p-hodnoty existuje spousta statistických dezinformací a proto si ji pojďme hezky vysvětlit.

P-hodnota je pravděpodobnost, že získáme danou hodnotu testové statistiky nebo extrémnější za předpokladu platnosti nulové hypotézy.

Lze si to přeložit taky následovně. P-hodnota nám říká, jak pravděpodobná jsou naše vzorová data, pokud je nulová hypotéza správná.

V případě našeho příkladu lze p-hodnotu spočítat například v Excelu, či jiném programu (ručně bych se do toho nepouštěla). V Excelu se bude jednat o následující zápis: 2*(1-NORM.S.DIST(ABS(z);1)), kde z = testové kritérium. V případě jednostranné hypotézy se výsledek nenásobí dvěma.

V našem případě vychází p-hodnota = 0,03.

Pojďme si ji vysvětlit v kontextu definice. Pravděpodobnost, že získáme danou hodnotu testové statistiky nebo extrémnější za předpokladu platnosti nulové hypotézy je 3 %.

Tedy pokud H0 platí, tak hodnotu -2,17 nebo extrémnější, získáme s pravděpodobností 3 %.

Pojďme zpět k testování hypotéz

Při každém testování hypotéz pracujete s hladinou významnosti. U nás je to 5 %, lze si to představit jako prostor tvořící kritický obor a zbylých 95 % je prostor oboru přijetí. Pokud je naše p-hodnota menší než hladina významnosti, tak logicky nulovou hypotézu zamítáme, naopak pokud je p-hodnota vyšší než hladina významnosti, tak nulovou hypotézu nelze zamítnout na dané hladině.

P-hodnotu lze vidět na grafu níže. Jelikož pracujeme s oboustrannou alternativní hypotézou, tak 5 % rozdělíme opět na dvě strany, tedy 2,5 % nalevo a 2,5 % napravo. P-hodnotu 3 % je rovněž nutné rozdělit na 1,5 % a 1, 5 % na obě strany.

Pokud by naše p-hodnota byla například 0,08 (8 %), tak by na každé straně byla 4 %, jednalo by se o vyšší hodnotu, než je uvedených 2,5 % a tedy bychom nemohli H0 zamítnout. Pravděpodobnost, že získáme danou hodnotu testové statistiky nebo extrémnější za předpokladu platnosti nulové hypotézy by byla 8 % a to je už příliš vysoká pravděpodobnost na to, aby se H0 mohla zamítnout.

V našem příkladu jsme došli k závěru, kdy se nám podařilo H₀ na 5% hladině významnosti zamítnout a přijmout H₁. Znamená to, že na 5% hladině významnosti se nám podařilo prokázat, že průměrná váha koblih je statisticky významně odlišná od 65 gramů. Váš pocit o změně váhy koblih je v tomto případě správný :).

Ráda bych zmínila, že v rámci testování hypotéz je nutné dodržet jistou terminologii a vyhnout se závěrům jako zamítáme H₁, nezamítáme H₁ a přijímáme H₀. Neexistuje žádný formální výsledek, který by na základě vzorku dat říkal, že „H0 přijímáme“, my v případě nezamítnutí H₀ pouze neprokážeme významný rozdíl.

Pojďme podívat na nejčastější dotazy ohledně testování hypotéz: